
[latexpage]
Ano de Copa do Mundo é ano do tradicional álbum de figurinhas. Nada mais empolgante do que completar o álbum e torcer para a seleção brasileira ser campeã, para imortalizar aqueles pedaços de papel colados em um livro de quase 80 páginas.
Bom, dado uma restrição orçamentária, me peguei perguntando quanto custaria entrar nessa brincadeira, com a expectativa de ir até o fim, é claro. Em outras palavras, quanto custa (em média) completar o álbum da Copa?
Bem, esse é uma questão que já foi bastante abordada na rede e talvez você já tenha achado outros links tratando do assunto, mas devemos ressaltar que há diversas formas de encará-lo.
Fora da internet, esse é um problema que já foi bem tratado pela matemática e estatística, sendo conhecido como Coupon collector’s problem, que na verdade trata da coleção de qualquer coisa, colocando as figurinhas como um caso particular do problema.
Bem, o atual álbum é composto por 682 figurinhas, obtidas em pacotes que custam R\$ 2,00 e que contem 5 figurinhas. O custo médio por figurinha, portanto, é de R\$ 0,40.
Se nunca viesse figurinhas repetidas, ou você pudesse comprar todas de forma avulsa por esse preço, o custo de completar o álbum seria de R\$ 252,80 (sem considerar o quanto você pagou no próprio álbum).
Como a graça do negócio é justamente demorar para completar, você vai conviver com um grande número de figurinhas repitidas e é daqui que vamos partir para a solução do nosso problema: quanto temos que gastar para completar um álbum.
A lógica é a seguinte, imagine que inicialmente você compre 8 pacotes e consiga 40 figurinhas, e nenhuma repetidas.
Quantos pacotes novos eu preciso comprar até ter uma figurinha que eu não tenho, dado que já tenho tais 40? Vamos chamar essa incógnita de $F_{40}$. Sendo assim, a quantidade necessária que eu preciso comprar dado que tenho 0 figurinhas será $F_{0}$, ou então dado que eu tenho 5 figurinhas $F_{5}$ e assim por diante.
Desta forma, a quantidade de figurinhas que preciso para completar o álbum é dado pela equação abaixo, utilizando a lógica introduzida acima:
$$F=F_{0}+F_{1}+F_{2}+F_{3}+…+F_{680}+F_{681}$$
Então $F$ será o total de figurinhas necessária que devemos adquirir para completar o álbum. O leitor certamente percebeu que entre 0 e 681 temos exatamente nossas 682 figurinhas.
Basta agora computarmos cada $F_i$ e somá-los. Mas como? Bem, vamos imaginar que você já rodou bem seu álbum e tem 250 figurinhas coladas, e agora você que a sua 251ª figurinha não repetida. Quando você abre o pacote, você tem para cada figurinha 682 possibilidades envolvendo cada jogador, seleção, escudo e etc.
A próxima figurinha não-repetida será dada pela seguinte fórmula, que na verdade é uma média, apresentada pelo pessoal do Numberphile:
$$F_{250}=\frac{250(F_{250}+1)+432(1)}{682}$$
Resolvendo essa equação para $F_{250}$ vem que $F_{250}=\frac{682}{432}$ ou seja na próxima 1,41 figurinha eu terei uma nova (ou melhor, a segunda figurinha que você adquirir tende a não ser repetida).
Dessa equação, conseguimos generalizar para qualquer montante que você já tenha: $F_{i}=\frac{682}{682-i}$ dessa fórmula é imediato ver que se você não tem nenhuma figurinha e está começando o álbum ($F_0$), a próxima garantidamente é não repetida (óbvio!).
Assim, para acharmos aquele somatório que envolve $F$, ou seja, o número total de figurinhas necessárias para completar o álbum, podemos aplicar a fórmula e chegar em:
$$F=\frac{682}{682}+\frac{682}{681}+…+\frac{682}{2}+\frac{682}{1}=4844$$
Portanto, para você completar o álbum da copa sozinho terá que adquirir algo como 4844 figurinhas, que são possíveis comprando 969 pacotinhos e gastando em torno de R\$ 1.938,00. Caro essa brincadeira, não?
Se você tem curiosidade por saber quantas figurinhas você ainda precisa adquirir, o simples código de R abaixo pode resolver seu problema, bastando substituir em $n$ o número de figurinhas que já tem e ele vai te devolver o quanto precisa para completar.
[sourcecode language=”r”] n<-681 d<-numeric() for(i in 0:n){ d[i]<-682/(682-i)} sum(d) [/sourcecode]A última figurinha não repetida é mais difícil de conseguir sendo necessários 682 novas até consegui-la. Sabendo disso, a produtora do álbum te da a possibilidade de comprar as últimas 50 figurinhas que você não tem, portanto nosso problema terminaria em $F_{631}$ e conforme o código abaixo,
[sourcecode language=”r”] n<-631 d<-numeric() for(i in 0:n){ d[i]<-682/(682-i)} sum(d) [/sourcecode]demandaria um total de 1774,7 figurinhas para completar o álbum do zero, ou seja, só de poder comprar as últimas 50 a quantidade necessária para completar tudo caiu mais do que pela metade. Agora temos que gastar em torno de R\$710,00 para completar e não mais os R\$ 1.938,00.
Bem, o problema não acaba ai, pois estamos considerando que você vai entrar nessa empreitada sozinho, ou seja, não vai em roda de amigos ou na banca da esquina fazer trocas.
Se colocarmos isso no problema, a equação muda, sendo necessário bem menos para completar o álbum. Esse problema foi estudado pelo falecido matemático Donald J. Newman, de Harvard, em seu trabalho “The Double Dixie Cup Problem“, que nos deu essa horrível equação abaixo (e adaptada por mim):
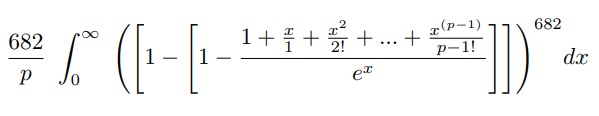
onde $p$ é o número de players, ou de amigos, que estão na roda de troca. Dessa forma, podemos ver abaixo que conforme $p$ aumenta, você precisa de bem menos figurinhas, mostrando quão importante é você ir em rodas de troca.

Editor do Terraço Econômico






Um Comentário