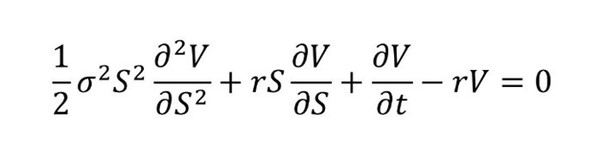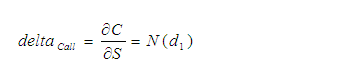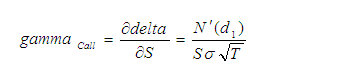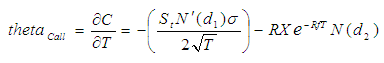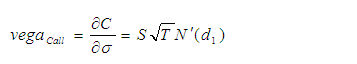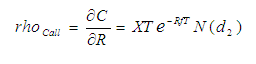
Black-Scholes, Gregas e Gênios – Parte I
Finalmente, as Gregas.
As gregas nada mais são que as variáveis derivadas da fórmula Black & Scholes, e que buscam medir a sensibilidade e o comportamento do preço da opção em relação a quatro fatores, ou seja, demonstram como o valor da aposta varia ao longo do tempo:
Cada grega mede um aspecto diferente na formação do preço da opção e somadas são utilizadas para encontrar ao preço “justo” da opção:
Delta – Mudança no Preço do ativo subjacente
O delta de uma opção mede a sensibilidade de seu preço em relação ao preço do ativo objeto do contrato, podendo ser entendido como um indicativo da exposição as oscilações no preço deste ativo no mercado à vista.
Talvez uma das gregas mais relevantes, é apresentada em termos monetários, demonstrando qual deverá ser a variação do preço da opção (ou de uma posição), caso ocorra uma variação de R$ 1,00 no preço do ativo.
Exemplo: Imagine que a opção esteja custando $17,00 e o Delta para esta opção é igual a 37%, isto quer dizer que para cada variação de $1 na ação a opção irá valer $17,37, ou seja, o valor da sua aposta ficará mais caro em R$ 0,37, provavelmente por que o preço da sua aposta está muito próximo de se tornar realidade.
Sendo assim, quanto maior o delta, mais próximo da sua aposta ser factível, e quanto menor o delta, mais distante e agressiva é sua aposta, e sendo assim, o valor justo pego para aposta (o prêmio) será menor.
Gamma
O Gama nada mais é que a segunda derivada do Delta, utilizada para testar a sensibilidade do delta em relação ao preço do ativo no mercado. Nada mais é que a medida de aceleração (a mesma da física) de qual velocidade o Delta pode chegar até 100%, sendo assim, quanto maior o Gamma, mais rápido sua aposta pode chegar a valer a pena, ou “dentro do dinheiro” no jargão de mercado.
Theta – Mudança no Tempo
O Theta mede a sensibilidade do preço da opção na passagem do tempo. É uma boa medida do que se costuma chamar de time decay: algo como a corrosão do tempo, pois pense que se você faz uma aposta para daqui 3 meses e cada dia que passa, se sua aposta não começar a chegar próximo do valor que você julgou, ela irá perder valor de mercado e será cada vez menos possível de acontecer, ou o contrário, irá se valorizando para cada vez mais próximo do seu vencimento, pois você o preço do ativo está chegando próximo do que você apostou.
Vega – Mudança na Volatilidade
O Vega mede a sensibilidade do preço da opção as variações na volatilidade implícita do ativo objeto no mercado à vista. O Vega normalmente é padronizado no mercado para refletir a variação no preço da opção dada uma alteração de 1% na volatilidade implícita pelo mercado de opções.
Dito em outras palavras, se uma ação tem uma grande variação no mercado a vista, se ela varia entre R$ 0,01 e R$ 10,00 em menos de 3 meses, as chances da sua aposta se concretizar é maior e então o preço da sua aposta (prêmio) será mais caro. O contrário também é valido, um ativo que é muito estático e com poucas oscilações tem menores chances de alcançar valores extremos que podem ser apostados.
Rho – Mudança na Taxa de Juros
O Rhô é a medida de sensibilidade do preço da opção as variações na taxa de juro sem risco da economia, no caso brasileiro, a sensibilidade a Taxa SELIC.
De uma forma geral verifica-se que o preço das opções é muito pouco sensível às mudanças nas taxas de juro, já que raramente são observadas alterações bruscas significativas no juros básico da economia. Pode-se verificar o comportamento do Rhô para as opção de compra de um modelo Black & Scholes, em relação à passagem do tempo e ao movimento do preço do ativo objeto.
A realidade como ela é e as limitações do modelo
Vale citar que apresentamos aqui apenas as gregas “básicas”, o modelo de Black & Scholes é muito extenso e complexo, o que permite encontrar várias outras gregas de segunda ou terceira ordem, que irão testar a sensibilidade das anteriores (são elas: Vanna, Charm, Vomma, Veta, Speed, Zomma, Color e Ultima), um prato cheio para quem gosta de matemática.[1]
Voltando às nossas perguntas iniciais:
Qual a probabilidade de nevar na região do Nordeste brasileiro?
Qual a probabilidade de você ganhar sozinho em sorteio da loteria?
Qual a probabilidade de um time da quarta divisão ser campeão da nacional?
Bem, a probabilidade é baixa, mas agora já sabemos como podemos precificar o valor justo dessas apostas. Vale citar que nesse caso, o valor do prêmio dessas opções seriam muito baixos, por conta de todos os fatores acima citados e por isso essas opções seria bem baratas, conhecidas como “pozinhos” em jargão de mercado, coisa de centavos e podem proporcionar retornos enormes (caso você acerte). Vale lembrar opções também são uma forma de buscar proteção ao seu portfólio de investimento, algo parecido ao comprar um seguro contra possíveis oscilações de mercado.
Outro ponto importante é que o modelo Black & Scholes é um ótimo para calcular opções dentro do dinheiro (próximas ao valor de exercício), porém não é tão ideal para calcular opções fora do dinheiro (longe do valor de exercício), apresentando diferenças substanciais entre o preço que o modelo aponta e o preço real da opção.
O modelo busca representar quantitativamente a realidade e não mensura variáveis subjetivas. Variáveis como: notícias políticas, o achado de uma nova bacia de petróleo ou uma crise de crédito em determinado país, e como as opções fora do dinheiro são as mais sujeitas a variações da volatilidade e pela grande probabilidade de não serem exercidas o modelo geralmente não as precifica corretamente.
Na prática, a utilização do modelo pelos operadores adquire uma práxis peculiar, nas palavras de Hull (1998, p. 557):
[…] fica evidente que o modelo Black-Scholes proporciona uma descrição menos que perfeita do mundo real. Os preços das ações e de outros ativos exibem um comportamento mais complexo do que o movimento browniano geométrico. Por que, então, profissionais de mercado continuam a utilizá-lo?
Um motivo é a facilidade de sua aplicação. Há apenas um parâmetro que não é observável no mercado – a volatilidade. Os profissionais podem, de forma não-ambígua, deduzir volatilidades a partir dos preços das opções e preços das opções a partir das volatilidades.
[…] Outro motivo da popularidade do modelo Black-Scholes reside no fato de os profissionais terem desenvolvido o que podemos chamar de “manhas” para lidar com suas imperfeições.
Os gênios, famosos desenvolvedores desse maravilhoso teorema: Louis Bachelier, Sheen Kassouf e Ed Thorp, Fischer Blacke e Myron Scholes decidiram sair da vida acadêmica para tentar a sorte no mercado financeiro e criando o seu próprio fundo de investimento, o famoso Long Term Capital Management (LTCM). Aplicaram assim seu modelo na realidade, operando opções de títulos públicos de diversos países.
A estratégia apresentou retornou gigantescos nos primeiros anos e o fundo chegou a possuir mais de 4bi de dólares sob gestão, mas não sobreviveu aos impactos da crise russa e depois a asiática, pois até os gênios falham e esse é um assunto para um próximo artigo.
[1] The Pricing of Options and Corporate Liabilities
Hull, J. (1998) – Opções, futuros e outros derivativos, BM&F, São Paulo, 3ª ed.
Black, F. & Scholes, M. (1972) – “The valuation of option contracts and a test of market efficiency”, Journal of Political Economy, Chicago, v.27: 497-505.
Costa, C. L. (1998) – Opções: operando a volatilidade, Bolsa de Mercadorias & Futuros, São Paulo
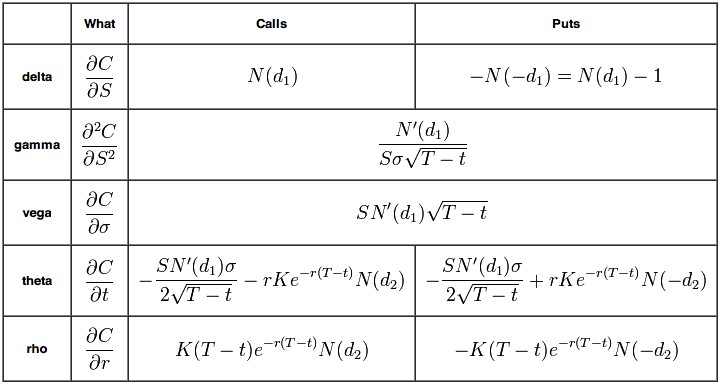
Tabela resumo sobre as principais gregas: