<![CDATA[
Em outras oportunidades aqui no Terraço Econômico[1], abordamos o tema da formação da curva de juros de uma economia e utilizamos a brasileira como exemplo. Além do conceito de taxa SELIC, explicamos que a formação da curva de juros está ligada a fundamentos macroeconômico: a percepção de risco e o valor do dinheiro no tempo. Interpolando as taxas para os diversos vencimentos, encontramos a estrutura a termo da curva de juros, algo semelhante à imagem abaixo.
Em tempos de revolução tecnológica e com todas as vantagens oferecidas pelos softwares de programação, por que não inserimos mais uma dimensão na curva de juros? Assim, poderemos visualizar a estrutura a termo para cada instante de tempo, isto é, para cada dia. Combinados em uma única estrutura, os eixos formarão uma superfície no espaço tridimensional.
Ensinaremos os nossos leitores a desenhar esta curva. Para tal tarefa, utilizaremos o famoso e maravilhoso software de estatística R (The R Project for Statistical Computing)[2]. Começaremos baixando e carregando o pacote Plotly[3]:
[sourcecode language=”r”] # Instalar o pacote plotly install.packages("plotly") # Carregar para o ambiente library(plotly) [/sourcecode]Agora, leremos os dados de dois arquivos. Um deles, que você pode encontrar aqui, contém as datas e os vencimentos, ou seja, os valores do eixo x e y, respectivamente. O outro arquivo, que disponibilizamos aqui, possui os valores do eixo z, as taxas de juros. Esses dados podem ser obtidos no site da ADVFN (cotações de contratos de DI de diversos vencimentos, dos anos de 2014, 2015, 2016, 2017 e 2018)[4].
[sourcecode language=”r”] xy <- read.csv("xy.csv", stringsAsFactors = F) # Transformaremos z em matriz porque a função # que usaremos depois exige esse formato z <- as.matrix(read.csv("z.csv", header = F, stringsAsFactors = F)) [/sourcecode]Precisaremos tratar ligeiramente os dados, transformando as cadeias de caracteres de datas em objetos data e removendo elementos vazios do vetor de vencimentos.
[sourcecode language=”r”] xy$data <- as.Date(xy$data, format = "%m/%d/%Y") y <- xy$data x <- as.vector(na.omit(xy$vencimento)) [/sourcecode]Finalmente, chamaremos o comando do Plotly para criar nossa curva de juros em três dimensões. A saída é exibida logo abaixo do código. Arrastando o mouse, você pode mover o gráfico em todas as direções para observar melhor a estrutura.
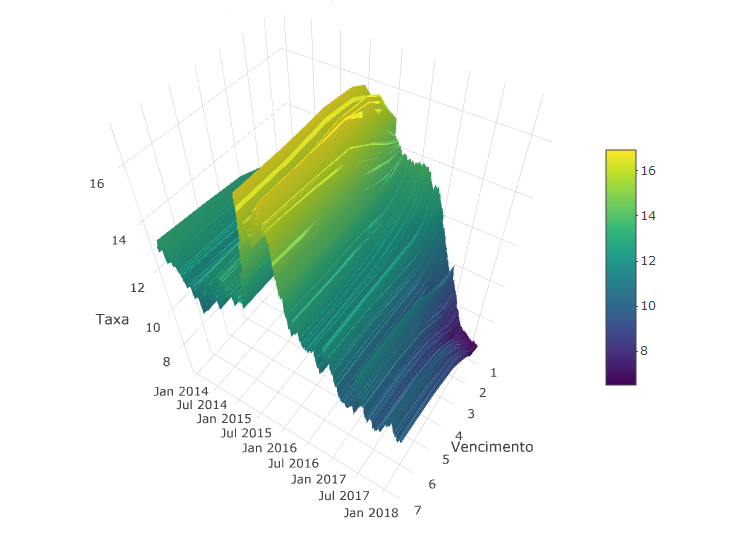
[sourcecode language=”r”] p <- plot_ly(x = x, y = y) %>% add_surface(z = z) %>% layout( title = "Curva de Juros 3D", scene = list( xaxis = list(title = "Vencimento"), yaxis = list(title = ""), zaxis = list(title = "Taxa") )) p [/sourcecode]Note como é impressionante como fomos do céu ao inferno em um período tão curto. O alta volatilidade e amplitude das taxas no período recente é evidente. Vamos analisar isso mais de perto, quebrando o gráfico em três grandes blocos.
- Janeiro 2014 – Abril 2015: O modelo econômico petista começava a dar seus sinais de fraqueza e a curva de juros como um todo operava em patamares elevados, entre 11%a.a. a 13%a.a., oscilando em torno de uma tendência crescente. As razões pelas quais o BC precisava elevar a taxa de juros no futuro eram muitas: proximidade da corrida eleitoral, sinais negativos vindos da política fiscal sustentável e a falta de credibilidade do próprio BC.
- Abril 2015 – Fevereiro 2016: Um verdadeiro drama. Época de reeleição, crise política, Lava-Jato e o gran finale, o impeachment. A curva como um todo se eleva em uma velocidade nunca antes vista. Saímos de 13%a.a. nos vencimentos mais curtos para 16%a.a. em todos os vencimentos. Mesmo que a SELIC tenha alcançando seu máximo em 14.25%, o mercado ainda acreditava em taxas de juros mais altas, com mais inflação desancorada, mais incerteza e maior risco em todo cenário, para qualquer prazo.
- Fevereiro 2016 – Fevereiro 2018: Outra grande mudança. Após a troca de governo, a implementação do teto de gastos e o inicio do ciclo de cortes da taxa de juros levaram a taxa a patamares baixíssimos. A parte curta da curva flutua hoje próxima a 6.5% a.a. e a parte longa está um pouco mais inclinada, próxima a 9.9% a.a.. Um bela diferença, comparada ao período anterior.
Fica nítido, observando a estrutura da curva como uma superfície dinâmica, que fazer politica monetária ou qualquer tipo de previsão de longo prazo no Brasil é, no minimo, desafiador. Contudo, a curva em três dimensões nos revela novos detalhes, ajudando na compreensão do que já ocorreu e de onde estamos agora.
Pedro Lula Mota & Talitha Speranza
[1] Nosso artigo: Entendendo a Curva de Juros Privada
[2] https://www.r-project.org/
[4] Cotações vencimentos de DI: https://br.advfn.com/investimentos/futuros/di-depositos-interfinanceiros/cotacoes