
“O evento mais espetacular da última metade do século passado é um que não ocorreu. ” (Thomas Schelling, An Astonishing Sixty Years: the Legacy of Hiroshima, 2005)
O que levou a União Soviética e os Estados Unidos a terem acumulado um grande arsenal nuclear sem isso acarretar em uma Guerra nuclear? Poderiam as ações desses países, que mais pareciam um suicídio global, serem entendidas como racionais? Seriam as guerras atos racionais? Robert Aumann defende que, se assim a entendermos, talvez seja mais fácil encontrar uma alternativa a ela (Aumann, 2005).
O matemático israelense-americano Robert J. Aumann e o economista americano Thomas C. Schelling dedicaram sua carreira a estudar a ação estratégica de diferentes agentes sob a ótima da racionalidade. Foi devida à contribuição de ambos para a compreensão dos conflitos e da cooperação, por meio da teoria dos jogos, que os mesmos foram premiados pela Real Academia Sueca de Ciências com o prêmio Nobel de Economia em 2005.
Robert Aumann nasceu no ano de 1930 em Frankfurt, na Alemanha e, aos oito anos, mudou-se com sua família para Nova Iorque. Ele completou seu Phd em matemática no MIT em 1955 e, no mesmo ano, ingressou em um centro afiliado à Universidade de Princeton onde trabalhou com aplicações matemáticas a questões industriais e militares. No ano seguinte, ele mudou-se para Israel e tornou-se professor do Instituto de Matemática da Hebrew University onde lecionou até usa aposentadoria no ano 2000 (Neymann, 2006).
Thomas Schelling nasceu em 1921 na Califórnia, Estados Unidos. Graduou-se na Universidade da Califórnia (Berkeley) e obteve seu Phd em 1951 pela Universidade de Harvard. Antes da carreira acadêmica, Schelling trabalhou no Departamento de Orçamento dos EUA (1945–46), na elaboração do Plano Marshall (1948-50) e no escritório executivo da presidência dos Estados Unidos (1951-53). Já em 1953 retornou à academia como professor da Universidade de Yale onde permaneceu até 1958, quando mudou-se para Harvard. Schelling também trabalhou para a RAND Corporation onde desenvolveu sua análise da corrida nuclear que culminou na publicação de sua obra mais conhecida “The Strategy of Conflict”. O economista também assessorou o governo de Kennedy na crise de Berlim no ano de 1961. Nos anos 90, Schelling ingressou como professor na Universidade de Maryland onde lecionou até sua morte no ano de 2016.
Ação Racional e Teoria dos Jogos
Antes de expor a contribuição de cada autor, vou dedicar essa introdução a falar um pouco sobre como entendemos racionalidade dentro da economia. Aumann define que o comportamento de um indivíduo é considerado racional se é do seu melhor interesse, dadas as informações disponíveis (Aumann, 2005). Em um mundo sem incerteza, a ação racional se baseia em selecionar dentro de um conjunto de alternativas factíveis aquela cuja consequência é a preferida em termos da sua utilidade. Já em um mundo com incerteza, o agente maximiza sua utilidade esperada, ou seja, ponderada pelas probabilidades, objetivas ou subjetivas, que atribui aos estados. A teoria econômica é fundamentada na ideia que os agentes (consumidores, firmas etc) se comportam de maneira racional. Com esse ferramental teórico, os economistas são capazes de realizar previsões sobre quais ações serão tomadas.
Contudo, o que ocorre quando as consequências de nossas ações também dependem das ações de outros indivíduos? Para modelar decisões estratégicas, os economistas usam da Teoria dos Jogos. Ela aplica a mesma lógica de ação racional que foi apresentada acima, porém se é considerado a melhor decisão que um agente pode tomar dada a ação de outro agente (Alisson & Zelikow, 1999).
Acredito que a maneira mais didática de apresentar a Teoria dos Jogos a quem não está familiarizado com o conceito seja apresentando um exemplo. Um dos jogos mais famosos na literatura é o do “Dilema dos Prisioneiros”. Ele consiste em um jogo simultâneo, onde os agentes jogam uma vez e ao mesmo tempo. Nele, dois prisioneiros, comparsas em um crime, presos em celas diferentes e sem poder se comunicar, devem tomar uma decisão: confessar ou negar o crime. Se ambos confessam, os dois devem cumprir uma pena de 3 meses; se um confessa e outro não, o que confessou estaria livre, enquanto aquele que não confessou seria condenado a 6 meses de prisão. Se ambos negam, eles ficariam presos por 1 mês. Para visualizar melhor, o jogo pode ser representado pela seguinte matriz de pay-offs:

Como apontamos, uma maneira de prosseguir para a “solução do jogo” é considerar que o agente deve maximizar sua utilidade dada a decisão do outro agente. Caso o prisioneiro 2 confesse, para o prisioneiro 1 também será melhor confessar, pois a sentença de 3 meses é melhor que a de 6. Se o prisioneiro 2 nega, seu comparsa no crime estaria melhor confessando, já que assim ele estaria livre. Vemos, então, que independente da escolha do jogador 2, a melhor resposta para jogador 1 é confessar. A mesma lógica se aplica para a escolha do jogador 2 dado o que o jogador 1 faria. Dizemos então que ambos confessarem é um Equilíbrio de Nash. Contudo, ambos estariam melhor se eles negassem, pois assim eles passariam só um mês na prisão. Assim, se existisse a possibilidade de coordenação, ambos tomariam a decisão de negar.
Um aspecto crucial para a cooperação não ser adotada em equilíbrio é a característica do jogo de ocorrer uma única vez. Em jogos repetidos, é possível “punir” desvios da cooperação. Contudo, isso dependerá se o jogo ocorre um número finito ou infinito de vezes. Muitas vezes quando há um número finito, na última rodada, ambos jogadores tem incentivo a desviar pois não haverá mais possibilidade de punição. Contudo, se ambos sabem que ao final não irão cooperar, como punir desvios na penúltima rodada? Essa mesma lógica se aplica a todas rodadas anteriores e não é possível garantir cooperação nesses jogos finitos. Já em jogos infinitos, a cooperação é possibilitada pois, sem o horizonte do final do jogo, a ameaça de punição do desvio é crível.
Uma observação importante: quando lidamos com jogos dinâmicos, é necessário considerar que jogadores podem ser mais ou menos impacientes. Quando um jogador valoriza muito o presente, ter um resultado alto agora pode ser preferível a resultados de cooperação em um período infinito de tempo. Logo, se um indivíduo é muito impaciente, o resultado de cooperação pode não se manter (Aumann, 2005).
Em realidade, para os jogadores cooperarem, o jogo não precisa possuir infinitas rodadas, mas sim ser jogado um número indefinido de vezes. Até que um horizonte final não seja antecipado, a ameaça de punição ainda mantém os jogadores cooperando. Essas são variações do que é conhecido como um superjogo, ou seja, repetições infinitas/indefinidas de um jogo em particular. Um teorema importante que se baseia na ideia que acabei de expor é chamado Teorema Popular (Folk Theorem).
Teorema Popular: O resultado cooperativo do jogo G coincide com o equilíbrio do superjogo 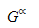
Após essa brevíssima introdução, podemos seguir com a explicação dos jogos desenvolvidos pelos vencedores do Nobel de 2005.
Robert Aumann
Apesar de conhecido desde o começo da década de 50 pelos teoristas dos jogos, o Teorema Popular não havia sido formalizado até Aumann (1959, 1960, 1961) escrever uma extensa análise dos jogos infinitamente repetidos (Hart, 2006).
Para compreender melhor a contribuição de Robert Aumann para a teoria dos jogos, vejamos um outro exemplo de Jogo proposto pelo matemático (Aumann, 2005). Dois jogadores, Rowena e Collin, devem decidir o quanto receberem. Rowena tem a opção de dividir, igualitariamente, de maneira que ela e Collin ganhem 10 cada um ou, ela pode optar por receber 10 vezes mais (100) enquanto Collin receberia 10 vezes menos (1). Simultaneamente, Collin decide se ele pune Rowena e, assim, ambos não recebem nada ou se ele concorda com a divisão. A matriz de pay off é tal que:
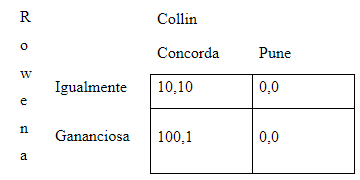
O melhor resultado para Rowena é ser gananciosa e conseguir um pagamento de 100. Já para Collin é melhor ele aceitar o acordo. Desse modo, quando as decisões ocorrem de maneira simultânea e o jogo não se repete, a divisão igualitária não se mantem em equilíbrio. Contudo, quando jogo é repetido, Collin pode ameaçar punir Rowena se ela desvia da divisão igualitária. Assim, em um jogo repetido infinitamente, a estratégia que ambos irão adotar é: Rowena divide igualitariamente e Collin aceita até que Rowena seja gananciosa. Caso isso ocorra, ele a pune daquele momento em diante. Contudo, poderíamos nos questionar até que ponto tal ameaça de punição de Collin é crível. Se Rowena desvia e Collin a pune desse período em diante, ele não estaria pior em comparação se não a punisse?
Caso você permaneça em equilíbrio após punir, ou seja, não há incentivo para desviar da punição, dizemos que estamos diante de um caso de Equilíbrio Perfeito. Uma das importantes contribuições de Aumann foi desenvolver o Teorema Popular Perfeito (Perfect Folk Theorem).
Teorema Popular Perfeito: Os resultados cooperativos do jogo G coincidem com os resultados de equilíbrio perfeito do seu superjogo 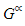
Esse Teorema se sustenta, pois Collin não precisa punir Rowena para sempre, ele pode punir até que a opção de desviar não seja mais lucrativa para ela. Para além disso, Rowena dividir de maneira gananciosa é em si uma “punição” por Collin não puní-la. Diante disso, Collin tem incentivos a optar pela punição. A opção por não desviar também é mantida quando, em vez de dois indivíduos jogando, temos um grupo de indíviduos. Se eles não conseguem obter benefícios ao não cooperar temos o resultado do Teorema Popular Forte (Strong Folk Theorem).
Na segunda metada da década de 60, Robert Aumann, Michael Maschler e Richard Stearns (1966, 1967, 1968) desenvolveram, através de uma pesquisa sobre a dinâmica das negociações do controle de armas, as bases da Teoria dos Jogos Repetidos com Informação Incompleta. Quando falamos em informação incompleta queremos dizer que um jogador não possui todas as informações relevantes para tomada de decisão. A exemplo, um país pode não ter conhecimento do arsenal militar de seu rival. Nesse caso, como o país melhor informado pode usar dessa vantagem? Quando temos um jogo de somente um período é trivial pensar que a parte melhor informada iria usar dessa informação para obter o maior ganho possível. Contudo, em jogos repetidos, essa escolha é mais complexa. Por um lado, a parte melhor informada pode usar dessa informação para obter ganhos de curto prazo, mas corre o risco de revelar essa informação através de suas ações. Assim, o jogador bem informado quer usufruir ao máximo dessa informação privada, revelando-a o mínimo possível. Aumann, Maschler e Stearns contribuíram a esse dilema propondo um teorema onde, de maneira elegante, revelam precisamente a quantidade de informação ótima a ser revelada.
Os teoremas propostos por Robert Aumann ajudam a explicar diversos resultados que foram provados empiricamente como, por exemplo, que é mais difícil sustentar cooperação quando há muitos jogadores, quando os jogadores interagem com menor frequência e quando há um horizonte de término para aquela interação (BANK OF SWEDEN, 2005).
Thomas Schelling
Thomas Schelling, em sua obra mais famosa, “The Strategy of Conflict”, faz um estudo das estratégias de dissuasão na tensão nuclear entre EUA e URSS. O economista argumenta que, com a capacidade destrutiva do arsenal bélico dos países durante a Guerra Fria, não estaríamos mais diante de um “Jogo de Soma Zero”, ou seja, jogos onde o total da perda de um agente equivale ao ganho do outro. Em vez disso, o conflito se apresentava como uma dependência mútua dos agentes (no sentido que ambos tinham a capacidade de destruir seu rival) e, assim, nas palavras de Schelling, criava-se uma “parceria precária” (Schelling, 1960)
As situações de conflito também são entendidas como situações de barganha pelo autor, ou seja, cada parte geralmente busca um acordo que seja o mais favorável possível para si, ponderando que ter um acordo é melhor do que ter nenhum acordo. Para explicar melhor como o uso da teoria dos jogos pode ser aplicado a questões de conflitos militares e abordar as contribuições de Schelling, vejamos o seguinte jogo, da classe dos “jogos da galinha”:
Dois países discordam acerca do direito a um território. Diante dessa tensão eles devem escolher se mobilizam tropas ou não. Caso ambos países mobilizem suas forças, a probabilidade de guerra (um resultado indesejado) é alta. Já se ambos se abstêm de um avanço militar, a probabilidade de chegarem a um acordo pacífico sobre a divisão territorial (um resultado melhor que a guerra) é alta. Vejamos então a matriz de pay-offs para ajudar a ilustrar o jogo:

Onde A>B>C>0, ou seja, o melhor resultado é conquistar o território sem guerra, seguido de um acordo pacifico de divisão e depois perder o território mas não entrar em guerra. Por último, a pior consequência para ambos países seria a guerra. Um leitor poderia fazer a observação aqui, que a guerra poderia ser preferível ao seu rival obter o território enquanto seu país não mobiliza as forças. O país poderia passar por uma humilhação caso adotasse o comportamento “covarde”, de “galinha”. Isso é verdade em diversos casos, mas para esse jogo específico, queremos mostrar qual vai ser a decisão dos países quando a guerra fornece um resultado muito ruim (pense no potencial suicida de uma guerra nuclear entre EUA e URSS)
Qual é a solução desse jogo? Colocando-se na posição do país 1, se o país 2 avança é melhor para o país 1 se abster de mobilizar suas tropas. Contudo, se o outro país se abstivesse, era melhor para ele avançar. Essa regra de jogada dada a ação de outro jogador constitui uma estratégia que irá nos levar a dois equilíbrios de Nash em Estratégias Puras: (mobilizar, abster), (abster, mobilizar). Já quando atribuímos probabilidades à escolha de cada estratégia, teremos um equilíbrio de Nash em estratégias mistas onde a probabilidade de guerra é positiva.
Vamos voltar à discussão de racionalidade levantada no início do texto. Ao proceder para encontrar o Equilíbrio de Nash (EN) em um jogo, adotamos uma hipótese forte que os agentes têm crenças corretas acerca das estratégias dos rivais. Em especial diante de um caso de Equilíbrios de Nash múltiplos, como no exemplo acima, deve haver mais elementos que fornecem justificativas à possibilidade de ancorar uma expectativa. Assim, alguns mecanismos que permitem a coordenação podem surgir.
O conceito de Ponto Focal foi introduzido na Teoria dos Jogos por Thomas Schelling no seu livro “The Strategy of Conflict”. Ele é caracterizado por algum conhecimento comum ou elemento cultural que permite convergência para um Equilíbrio de Nash específico quando o jogo possui múltiplos EN. A exemplo, imagine que dois jogadores devem escolher entre uma categoria de Nobel tendo, assim, 6 Equilíbrios de Nash em Estratégias Puras (Física, Química, Fisiologia/ Medicina, Literatura, Paz e Economia). Somente se os dois escolherem a mesma categoria ganham um valor positivo. Se os dois jogadores são leitores desse texto não seria provável pensar que eles escolheriam o Nobel de Economia? No contexto do jogo estudado, podemos pensar que se perturbarmos o jogo de modo que um país tenha mais a ganhar que outro com a mobilização, tornamos o Equilíbrio de Nash Puro (um avança e outro abstém) “focal”.
Uma outra importante contribuição de Schelling para a teoria estratégica moderna são seus estudos sobre a dissuasão. Suponha que o país 1 se comprometa, com probabilidade suficientemente alta, a mobilizar suas tropas caso o país 2 também mobilize. Essa ameaça garante então um “equilíbrio do terror”, pois a melhor resposta para os países será se abster de avançar. Uma das proposições mais relevantes de Schelling no estudo de conflitos é como a Guerra Nuclear seria evitada com a estabilidade do “equilíbrio do terror”, ou seja, se ao atacar um país, sou incapaz de destruir a capacidade dele contra-atacar (Alisson & Zelikow, 1999).
Agora imaginemos que estamos diante de um jogo de informação incompleta onde o país 1 não sabe se o pay-off da guerra é preferível ao da negociação para o país 2. Assim, o país 1 ainda iria se comprometer a mobilizar tropas se o país 2 as mobilizassem? Trazendo essa pergunta ao contexto da Guerra Fria, como fazer uma ameaça crível de iniciar uma guerra que pode acarretar em uma destruição mútua? Schelling argumenta que a estratégia ótima para o país 1 seria fazer ameaças que envolvam uma probabilidade de mobilização menor que 1. A ameaça de uma guerra nuclear pode não ser crível, mas o aumento do risco de uma guerra pode obter credibilidade.
Schelling defende que para deter então a mobilização do inimigo o país deveria adotar a estratégia de brinkmanship, ou seja, a “criação deliberada de um risco reconhecido e não totalmente controlável”. Uma vez que o país 2 tomasse consciência que o país 1 não tem mais controle da situação, a guerra é evitada somente com o país 2 se abstendo da mobilização.
Um caso histórico que serviu como um teste empírico para as formulações de Schelling foi a Crise dos Mísseis de Cuba, evento no qual a União Soviética e os Estados Unidos chegaram muito próximos a um conflito direto. Em outubro de 1962, os Estados Unidos obtiveram provas mais contundentes da instalação de mísseis balísticos soviéticos no país caribenho. Frente a tal ameaça nuclear, o alto escalão político/militar dos Estados Unidos chegou a planejar uma invasão a Cuba, mas o governo de Kennedy optou por um bloqueio ao país caribenho a fim de impossibilitar a chegada de mais armamentos soviéticos à ilha. Caso um navio ultrapassasse o limite estabelecido pelo bloqueio, os EUA tinham se compromissado com a possibilidade de interceptá-los por meio do uso da força. Contudo, ainda permanecia o dilema de como lidar com os mísseis já instalados na ilha. O governo dos Estados Unidos optou por demandar que eles fossem desmantelados e se comprometeram, em um anúncio público, que, se os mísseis soviéticos fossem usados contra os Estados Unidos, eles iriam retaliar (Alisson & Zelikow, 1999). Assim, alguns analistas defendem que as ações dos EUA seguiram uma estratégia de brinkmanship para resolução da Crise dos Mísseis.
No dia 28 de Outubro, Nikita Khrushchev anunciou a retirada dos mísseis soviéticos de Cuba. O episódio da Crise dos Mísseis incentivou Thomas Schelling a pensar em uma série de medidas para evitar a repetição de um jogo fadado a terminar em desastre, o que parecia ser o caso da Guerra Fria. Uma das sugestões de Schelling que veio a ser adotada pelo governo Kennedy foi estabelecimento de uma linha telefônica direta entre a Casa Branca e o Kremlin, o que ficou popularmente conhecido como o “telefone vermelho. ”
Críticas
Uma crítica comum feita à abordagem de ambos vencedores do Nobel de 2005 versa acerca da hipótese fundamental dos agentes serem racionais. Em verdade, quando trabalhamos com modelos teóricos em economia, nós adotamos uma simplificação da realidade. Como dizia o estatístico George Box (1956), “todos os modelos estão errados, mas alguns são úteis. ” No final, o julgamento de um modelo deveria se basear menos nas suas hipóteses per se e mais se são adequados para certas aplicações. Uma outra crítica feita é a falta de dados para comprovação empírica das análises de Schelling. À exceção de uma análise da Crise dos Mísseis de Cuba, os argumentos do economista estavam mais baseados em ilustrações e anedotas (Jordan, 2015).
Após os laureados de 2005 terem sido anunciados, a Real Academia Sueca recebeu uma petição assinada por mais de mil intelectuais de diversas nacionalidades criticando a entrega do prêmio para Robert Aumann e Thomas Schelling por suas posições políticas e pelas consequências de sua teoria. Aumann defendeu, por meio do ferramental da Teoria dos Jogos, a manutenção dos assentamentos israelenses na Faixa de Gaza a fim de que os Palestinos fizessem maiores concessões futuras. A política de assentamentos é amplamente criticada pela comunidade internacional e considerada uma quebra dos direitos de autodeterminação dos povos e soberania do povo palestino sobre seu território (UN, 2004). Já com relação a Schelling, a crítica foi no sentido da sua teoria defender o uso coercitivo da força militar e ter, assim, inspirado ações do governo americano como o bombardeamento do Vietnam do Norte a fim de pressionar Ho Chi Minh a retirar o apoio aos VietCongs.
Conclusão
Sob abordagens distintas, os dois vencedores do Nobel de 2005 trouxeram uma grande contribuição científica à análise de interações humanas por meio da teoria dos jogos. Aumann, por teoremas matemáticos e forte formalização, ajudou principalmente na compreensão de interações sociais de longo prazo através dos jogos não cooperativos. Já o destaque de Schelling não vinha da prova matemática de estratégias de conflito, mas sim da aplicação de uma teoria de racionalidade a situações da vida real (BANK OF SWEDEN, 2005). Apesar das críticas feitas às possíveis consequências negativas das análises de Schelling, muitos cientistas sociais defendem que seus estudos sobre as estratégias de dissuasão contribuíram para evitar a escalada nuclear durante o período da Guerra Fria.
Maria Oaquim de Medeiros
Formada em Economia pela PUC-Rio e mestranda em Economia pela mesma universidade.
Notas
ALLISON, Graham; ZELIKOW, Philip. Essence of Decision: Explaning the Cuban Missile Crisis. 2nd Edition. 1999
AUMANN R.J, MASCHLER, M (1966, 1967, 1968): “Game theoretic aspects of gradual disarmament”, “Repeated games with incomplete information: A survey of recent results”, and “Repeated games of incomplete information, the zero-sum extensive case”, Reports ST-80, 116 and 143, Mathematica Inc., Princeton, NJ.
AUMANN, R. J. (1959), Acceptable Points in General Cooperative n-Person Games, in A. W. Tucker and R. D. Luce (eds.), Contributions to the Theory of Games IV, Annals of Mathematics Study 40, Princeton University Press, Princeton, NJ, 287–324.
AUMANN, R. J. (1960), Acceptable Points in Games of Perfect Information, Pacific Journal of Mathematics 10, 381–417.
AUMANN, R. J. (1961), The Core of a Cooperative Game without Side Payments, Transactions of the American Mathematical Society 98, 539–552.
AUMANN, R. J., MASCHLER M.(with the collaboration of R. Stearns) (1995): Repeated Games with Incomplete Information, MIT Press.
AUMANN, R.J., MASCHLER, M., STEARNS R. (1968): “Repeated games of incomplete information: an approach to the non-zero sum case”, in Report of the U.S. Arms Control and Disarmament Agency ST-143, Chapter IV, 117-216.
AUMANN, Robert. War and Peace .Prize Lecture1, December 8, 2005.
BANK OF SWEDEN, Robert Aumann’s and Thomas Schelling’s Contributions to Game Theory: Analyses of Conflict and Cooperation. 10 October 2005
BOX, George (1976), “Science and statistics” (PDF), Journal of the American Statistical Association, 71 (356): 791–799.
HART, Sergiu. Robert Aumann’s Game and Economic Theory. Scandinavian Journal of Economics. 108 (2006),2,185-211.
JORDAN, Richard. An Essay on Thomas Schelling’s Arms and Influence. 2015
NEYMAN, Abraham. Aumann Awarded Nobel Prize. Notices of the AMS. volume 53, NUMBER 1, January 2006
SCHELLING T.C. (1960): The Strategy of Conflict, Harvard University Press, Cambridge MA.
SCHELLING, Thomas – BIOGRAPHICAL. NobelPrize.org. Nobel Media AB 2020. Sat. 15 Aug 2020 <https://www.nobelprize.org/prizes/economic-sciences/2005/schelling/biographical/>
SCHELLING, Thomas. AN ASTONISHING SIXTY YEARS: THE LEGACY OF HIROSHIMA. Prize Lecture, December 8, 2005
UNITED NATIONS, General Assembly, Status of the Occupied Palestinian Territory, including East Jerusalem. A/RES/58/292(17 May 2004). Available from: <https://unispal.un.org/UNISPAL.NSF/0/A2C2938216B39DE485256EA70070C849>
VARIAN, Hal. Microeconomia: uma abordagem moderna. 9ª EDIÇÃO




