A teoria dos jogos e as vacinas

Apesar da primeira vacina ter sido criada em 1796 para prevenir a varíola, existem relatos de que a inoculação de fluidos contaminados já era usado na China como prevenção de doenças desde o ano 1.000^[1]. Os avanços que as vacinas trouxeram para a saúde são inegáveis, basta olhar os gráficos de prevalência das doenças antes e depois do surgimento das vacinas,  a mudança de padrão fica clara como no exemplo abaixo:

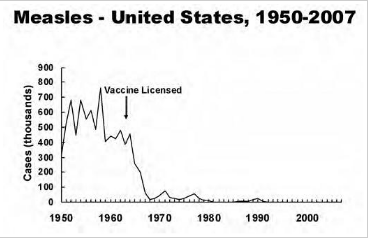
A vacinação é quase uma unanimidade na comunidade médica, basta dizer que 95% dos pediatras americanos seguem o calendário vacinal oficial nos seus próprios filhos^[1]. A grande parte dos 5% restantes apenas decide atrasar em alguns meses a vacinação contra algumas doenças. Apesar disso, é crescente^[2] o movimento, principalmente dos países desenvolvidos, de pessoas que decidem não vacinar os seus filhos.

Mas o que tem a ver o assunto vacinas em um site de economia? Eu resolvi trazer esse assunto aqui porque a decisão de vacinar ou não, apesar de ser uma decisão de saúde é também uma decisão ética que segue um modelo bastante semelhante com o famoso Dilema do Prisioneiro^[3], situação hipotética em que a maximização da utilidade dos agentes leva a diferentes cenários, e que curiosamente a situação ideal é quando ambos colaboram entre si, porém os incentivos a atitudes individualista é maior, caracterizando assim a questão central do dilema. Esse é o problema, os benefícios são dispersos e os custos concentrados, fenômeno semelhante de quando privatiza-se uma estatal, a população não percebe o benefício de forma clara, porém no agregado, seja com mais pessoas vacinadas ou com menos uma estatal, toda a sociedade é beneficiada.

Mas voltando ao exemplo das vacinas, para entender como isso funciona é preciso explicar os conceitos de cobertura vacinal e de imunidade de manada. A cobertura vacinal é o percentual de pessoas vacinadas em determinada região, já imunidade de manada é uma forma de proteção indireta que ocorre quando uma grande parcela de uma determinada população é vacinada. Assim, quanto maior o número de pessoas vacinadas, ou seja, quanto maior a cobertura vacinal, menor a probabilidade daqueles que não estão imunes (por não terem sido vacinados) contraírem determinada doença.

Para cada doença infecto-contagiosa podemos definir também 2 parâmetros matemáticos principais^[4], o  R0 e o HIT. R0 é o número médio de pessoas contaminadas a partir de um caso inicial de determinada doença, já o HIT (herd immunity threshold) é o percentual mínimo da população imune (ou por vacina, ou por já ter contraído a doença). Em geral, quanto maior o R0, mais fácil a propagação da doença e portanto maior deve ser a sua cobertura vacinal. Por exemplo: uma pessoa com sarampo contamina em média de 12 a 18 pessoas (R0), com isso, a imunidade mínima da população para controlar essa doença é de 92 a 95%. Já quem contrair Caxumba, contamina um número menor de pessoas (em média 4 a 7), requerido uma imunidade da população menor para o seu controle (HIT estimada em 75 a 86%)

Dessa maneira, se você não vacinar o seu filho, mas um percentual elevado de pais vacinar suas proles, o seu filho acaba se beneficiando indiretamente, tornado-se protegido sem correr o risco dos efeitos colaterais das vacinas (que apesar de serem seguras podem causar dor, febre e outros efeitos mais graves em casos raros).

Vamos resumir as decisões possíveis em uma matriz de resultados:

As pessoas que não vacinam os seus filhos, contam com o pressuposto de que a maioria irá  vacinar. É um pensamento individualista no qual a pessoa recebe o benefício sem correr riscos ou arcar com custos. Mas eticamente é justo que isso aconteça?

A maioria dos médicos defende que não. Para nós, a opção de não vacinar deveria ficar restrita as pessoas que por razão de saúde não podem tomar vacinas. Uma criança que nasceu com imunodeficiência, por exemplo, pode ficar doente de verdade com a vacina, já que o seu corpo não consegue combater nem os vírus ou bactérias atenuados presentes em algumas vacinas. Crianças em tratamento contra o câncer também sofrem desse problema, uma vez que o seu sistema de defesa fica debilitado durante o tratamento. Em ambos os casos, essas crianças além de não poderem tomar vacinas, ainda estariam sujeitas a sofrerem as formas mais graves e fatais das doenças, caso a cobertura vacinal não seja suficientemente alta.

Por outro lado, muitas pessoas defendem que a decisão de vacinar é individual e que o Estado não pode obrigar os pais a darem injeções, que potencialmente pode causar efeitos colaterais graves (ainda que raros), em seus amados filhos.

Voltando ao Dilema do Prisioneiro, se um agente “trair” é considerado como a estratégia dominante, ou seja, ele irá obter melhor o resultado independente da decisão do outro jogador. Semelhante ao que ocorre aos pais que não vacinam e obtém o beneficio de protegerem seus filhos indiretamente.

Mas se então, se em caso todos os pais escolherem a estratégia dominante (e isso ocorrer de em grande escala), a doença irá se alastrar. Assim, dizemos que “Não vacinar – Não vacinar” é considerada como solução de equilíbrio ou Equilíbrio de Nash (sim, aquele do filme). O equilíbrio de Nash é a combinação de decisões em que nenhum jogador pode melhorar seu resultado com uma ação individualista.

Fato é que a solução de equilíbrio de Nash não é o melhor resultado, sendo que existe um outro possível e que gera maior benefícios. Assim, o Dilema dos Prisioneiros é uma abstração de situações comuns (no caso, das vacinas) onde a escolha do melhor individual conduz à traição mútua e consequentemente prejuízo em conjunto. Enquanto que a colaboração proporcionaria melhores resultados.

Entre a liberdade dos pais de decidir o que é melhor para os seus filhos e o bem comum que é manter a cobertura vacinal alta e proteger toda a sociedade o que deve falar mais alto?

Renata K. Velloso Médica, formada em administração pública, vive e trabalha na Califórnia.

Pedro Lula Mota Editor do Terraço Econômico

^[1] http://file.scirp.org/pdf/OJPed20120300003_46564276.pdf

^[2] http://www.mrt.com/news/article_55ca86be-b590-11e4-adaa-6f9d2386cf09.html

^[3] http://www.barrichelo.com.br/teoriadosjogos/list-trechosimprime.asp?id=29

^[4] https://en.m.wikipedia.org/wiki/Mathematical_modelling_of_infectious_disease

^[1] http://www.historyofvaccines.org/content/chinese-smallpox-inoculation