Uma das equações fundamentais da matemática pode ser dada por uma expressão. Essa equação é a base para várias áreas da ciência e sem ela nosso mundo contemporâneo jamais poderia ser da forma como ele é. Essa expressão é dada da seguinte forma:
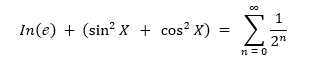
Essa equação é extremamente antiga. Foi por meio dela que, por exemplo, os antigos gregos conseguiram erguer o Partenon, que os romanos pavimentaram seu Império e por meio da qual as Grandes Navegações foram possíveis. No mundo atual, é indispensável que qualquer pessoa que busque uma posição analítica dentro de uma organização saiba dessa equação.
Mas afinal, caro leitor, o que essa equação nos diz? Você sabe?
Bem, para explorar essa relação tão fundamental é necessário entender os seus termos. O que cada um deles representa? Bem, o primeiro termo nada mais é do que o logaritmo natural do famoso número de Euler. Mas o que é um logaritmo natural? Um logaritmo natural é simplesmente uma função matemática que nos diz a que expoente um determinado número deve ser elevado para que outro seja obtido. Em outra palavras:
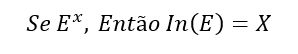
O número de Euler é bastante curioso. Suas propriedades estão entre as mais interessantes na matemática. Geralmente ele assume a forma aproximada de 2,71828, porém isso é irrelevante para nossa questão. Por qual razão? Devido o logaritmo natural do número de Euler ser simplesmente:
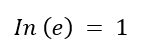
Muito bem, caro leitor, temos então nosso primeiro termo. E com relação ao segundo termo? Tal termo é meramente uma das propriedades fundamentais da trigonometria, a qual diz:
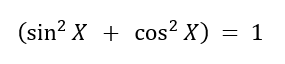
Assim temos que:
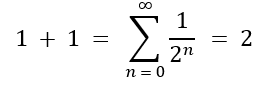
E sabemos que tal é verdadeiro, pois a soma de uma série geométrica infinita (o termo do lado direito da equação) é tal que:
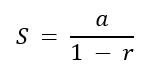
Onde S é a soma da série, a é o primeiro termo da série e r é a razão comum dos termos consecutivos ( ou seja, 1/2). Dessa forma termos que:
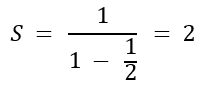
Sim, meus caros leitores, aquela equação rocambolesca inicial foi apenas para dizer que:
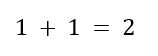
Mas por qual razão eu fiz você passar por essa loucura sem sentido nenhum? Observe que a minha narrativa no começo do artigo apontava essa equação como algo fundamental para a operacionalização do nosso mundo (e realmente é), porém eu apresentei ela em uma forma extremamente complexa.
Aposto que o que a maioria de vocês sentiu ao ver aquela equação horrível foi um pequeno pico de ansiedade, uma palpitação apertando o peito. É sobre esse sentimento que eu desejo refletir com vocês.
Veja, eu observo que cada vez mais estamos cercados por essas demonstrações rocambolescas de técnica. Basta abrir o Youtube ou qualquer rede de compartilhamento de conteúdo e você verá pessoas fabricando conteúdos com os seguintes enunciados “Essa mudança tecnológica irá mudar tudo!” ou então vídeos de supostos especialistas tratando de temas de finanças quantitativas construindo em torno do tema uma aura quase mística e arcana.
De um ponto de vista crítico, isso não passa da construção de máscaras por parte de supostos especialistas acerca de temas que, no fim das contas, não são tão difíceis e impressionantes a ponto de valer o louvor dedicado a essas mentes “iluminadas”. Como lógico eu não vejo substância nesse tipo de cultura, pois eu tendo a me pautar pelo mais velhos dos princípios da matemática: a simplicidade.
O conhecimento deve ser apresentado da maneira mais simples e objetiva possível, seja ele qual for. Como coloca o professor Ledo Vaccaro, a matemática pode ser difícil, mas ela é incrivelmente simples. Nenhum matemático que não almeja a simplificação de sua formulações deve ser levado a sério. De igual forma, um programa de computador construído sob um código complexo demais tende a falhar ou não ter aplicação prática devido impossibilidade de emulação e adaptação.
Se algo for passado ao público de forma complexa, quando poderia ser simples, tal indica que o agente transmissor daquela mensagem provavelmente está tentando enganar o público e se elevar sob um pedestal de areia.
Assim, da próxima vez que você vir um colega ou influenciador tentando sinalizar conhecimento ou expertise em determinado assunto peça que ele apresenta esse mesmo assunto da maneira mais simples que ele conseguir. Se ele não o conseguir explicar de maneira simples e lógica o assunto, você já deve levantar bandeiras vermelhas de que aquilo provavelmente é uma fraude.